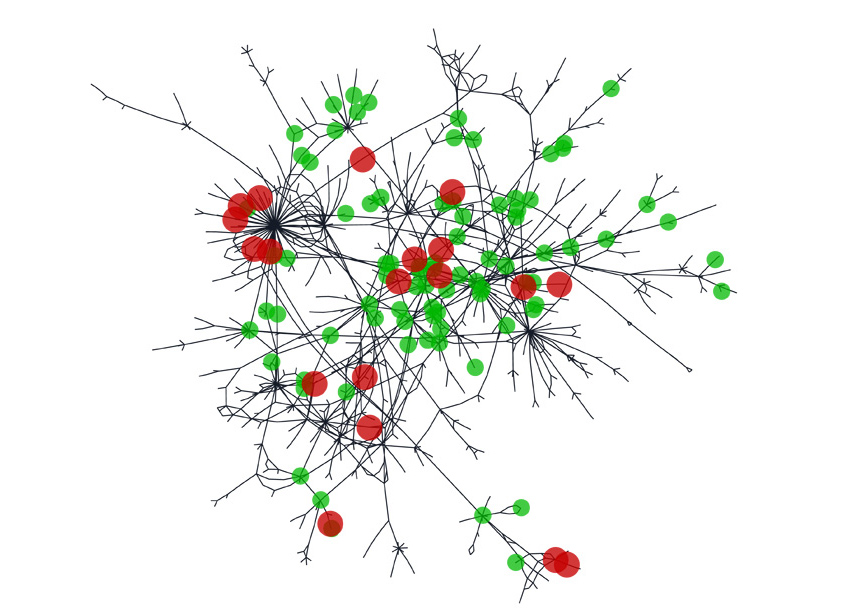
¿Se puede saber de manera precisa qué cadena de acontecimientos provoca la alteración de la concentración de metabolitos en el cuerpo una vez que se ha ingerido un medicamento? ¿O, por ejemplo, cómo se propagará una información confidencial en una gran empresa? Un grupo de investigadores de la Universitat Rovira i Virgili ha desarrollado una nueva herramienta, un algoritmo matemático basado en un modelo probabilístico, que identifica los caminos más probables de la red de interacciones entre las unidades de un sistema y proporciona estimaciones rápidas y precisas para tener información sobre las posibles trayectorias de propagación

Pongamos por caso que un individuo ingiere un medicamento y, horas más tarde, un análisis de sangre revela que la concentración de algunos metabolitos ha cambiado respecto a lo que sería habitual. Ante esta situación, el médico intenta interpretar la cadena de acontecimientos que traen estos cambios, pero se enfrenta a desafíos significativos. En primer lugar, hay miles de metabolitos y miles de reacciones bioquímicas que transforman unos metabolitos en otros. En segundo lugar, la estructura de la red metabólica se mantiene, pero las concentraciones de metabolitos han mutado por efecto de estas reacciones. En tercer lugar, el médico ignora el estado de la mayoría de los metabolitos, puesto que solo una parte de ellos, cerca del 10 %, se mide en un análisis de sangre. Con los datos que tiene a su alcance, el médico no puede responder a preguntas como, por ejemplo, qué reacciones han provocado que la modificación metabólica se haya extendido, o bien cuántos metabolitos, que no se pueden medir, se han visto afectados.

Investigadores del grupo de investigación SEES:lab, del Departamento de Ingeniería Química de la URV, junto con investigadores de la Unidad de Investigación Biomédica del Departamento de Medicina y Cirugía, han hecho frente a ese desafío y han comprobado los resultados en casos reales, con voluntarios que ingirieron un extracto de una planta para poner a prueba el resultado de un nuevo modelo matemático que han desarrollado. Se trata de analizar un volumen muy elevado de información, buscar las conexiones entre los nodos y, finalmente, darles más o menos relevancia. Todo ello lo han aplicado a problemas dinámicos para poder saber por dónde se ha propagado en una red una perturbación causada por factores externos; se trata, de definitiva, de conocer una parte para poder prever el todo.

En contraste con lo que pasa, por ejemplo, con la propagación de una epidemia —normalmente se tiene la información completa del estado de las personas dentro de una red—, las observaciones de determinadas modificaciones de una red dinámica suceden en poco tiempo, de modo que solo se puede hacer una observación parcial de ellas. Matemáticamente, se pueden encontrar soluciones a este problema dejando claro que las alteraciones se propagan siguiendo caminos en la red de interacciones entre las unidades del sistema (es decir, metabolitos, en el ejemplo estudiado). Un reto importante en muchas áreas, desde la biología hasta las ciencias sociales, es deducir las trayectorias de propagación de la observación de los efectos de las alteraciones.

Esta herramienta, por tanto, es capaz de prever la alteración de un red completa teniendo solo una parte de la información. Además, lo hace de forma automática y permite procesar un volumen muy elevado de información en poco tiempo. Los resultados sugieren que, más allá de prever las alteraciones en una serie de contextos, también se puede utilizar para guiar hipótesis y descubrimientos, por ejemplo, ayudando en la identificación de la ramificación de puntos de los trazados de una alteración.

Referencia bibliográfica: Francesco Alessandro Massucci, Jonathan Wheeler, Raúl Beltrán-Debón, Jorge Joven, Marta Sales-Pardo, Roger Guimerà. “Inferring propagation paths for sparsely observed perturbations on complex networks” Science Advances21 Oct 2016 : e1501638 DOI: 10.1126/sciadv.1501638